Оглавление

Приближенное вычисление определенного интеграла

Метод средних прямоугольников

Пусть на отрезке [a, b] задана непрерывная функция f(x). Требуется вычислить интеграл , численно равный площади криволинейной трапеции.

Разобьем основание этой трапеции на n равных отрезков длины d = (b - a)/n с помощью точек x0 = a, x1, x2, ... xn = b.

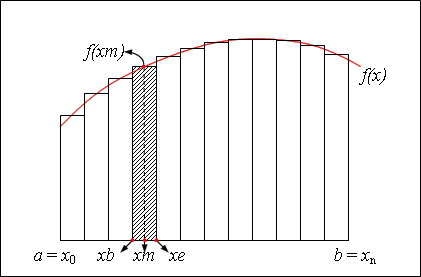
Приняв отрезки за основания, построим на каждом из них прямоугольник с высотой y = f(xm), где xm – точка, лежащая посредине отрезка: xm = (xa + xb)/2. Тогда площадь прямоугольника будет выражаться формулой: si = d* f(xm). Сумма площадей прямоугольников дает приближенное значение площади под графиком функции и, следовательно, приближенно равна искомому интегралу на отрезке [a, b].

Программа для вычисления

<script type="text/javascript">
a = 0;
b = 1;
n = 100;

s = 0;
d = (b - a)/n;
xb = 0;

	for(i = 0; i < n; i++){
		xe = xb + d;
		xm = (xb + xe)/2;
		s = s + d*xm*xm;
		xb = xe;
	}
	t = " Интеграл (x*x)  = " + s;
	document.write(t);
</script>

Данная задача имеет точное решение:

Самостоятельно модифицировать программу для вычисления интеграла

Программа для вычисления

<script type="text/javascript">
a = 1;
b = 2;
n = 100;

s = 0;
d = (b - a)/n;
xb = a;

	for(i = 0; i < n; i++){
		xe = xb + d;
		xm = (xb + xe)/2;
		s = s + d*Math.log(xm) ;
		xb = xe;
	}
	t = " Интеграл (log(x))  = " + s;
	document.write(t);
</script>

Данная задача имеет точное решение:

А вот следующая задача точного решения уже не имеет. Интеграл носит название интеграла Пуассона. Он не выражается через элементарные функции и его значения можно рассчитать только используя приближенные методы.

Программа для вычисления

<script type="text/javascript">
a = 0;
b = 2;
n = 100;

s = 0;
d = (b - a)/n;
xb = a;

	for(i = 0; i < n; i++){
		xe = xb + d;
		xm = (xb + xe)/2;
		s = s + d*Math.exp(-xm*xm); 

		xb = xe;
	}
	t = "<p> Интеграл (exp(-xm*xm))  = " + s + "</p>";
	document.write(t);
</script>

Интеграл Пуассона используется в теории вероятности и его принято записывать в виде функции верхнего предела

Следующая программа вычисляет значения функции Пуассона на отрезке [0, 2] с шагом 0.1

<script type="text/javascript">
var mx = new Array(); // Объявление массива значений аргументов
var my = new Array(); // Объявление массива значений функции

	dx = 0.1;
	a = 0;
	b = dx;
	n = 100;

	k = 1/(Math.sqrt(2*Math.PI)); //Коэффициент перед интегралом Пуассона

	for(j = 0; j < 20; j++){ // Изменение верхнего предела интегрирования
		s = 0;
		d = (b - a)/n;
		xb = a;

		for(i = 0; i < n; i++){ // Вычисление интеграла в указанных пределах интегрирования
			xe = xb + d;
			xm = (xb + xe)/2;
			s = s + d*Math.exp(-xm*xm/2); 

			xb = xe;
		}
		mx[j] = b;
		my[j] = k*s;
		b = b + dx;
	}

	for(j = 0; j < 20; j++){ // Вывод результатов на экран
		t ="<p> x  = " + mx[j] + "  y  = " + my[j] + "</p>";
		document.write(t);
	}
</script>

Для хранения вычисленных значений аргументов и функций используются два массива mx и my. Перед использование массивы необходимо объявить. Это делается при помощи инструкций:

var mx = new Array(); 
var my = new Array(); 

После объявления к элементам массивов можно обращаться при помощи индексов. Например, для того чтобы записать информацию в i-ый элемент массива мы используем следующую запись: mx[i] = b; А для того, чтобы прочитать информацию из j-ого элемента мы должны записать: y = my[j];

Создаем подпрограмму для вычисления интеграла от произвольной функции, заданной пользователем

<script type="text/javascript">
var a, b, n, f;

a = 2;
b = 5;
n = 100;
f = "1/log(x)";

integral(a, b, n, f);

function integral(a, b, n, f) {
var s, d, xb, xe, x, t;
s = 0;
d = (b - a)/n;
xb = a;
t = f;
f= "with (Math) {" + f + "}";
	for(i = 0; i < n; i++){
		xe = xb + d;
		x = (xb + xe)/2;
		s = s + d*eval(f);
		xb = xe;
	}
	t = " Интеграл от " + t  + "  = " + s;
	document.write(t);
}//function integral

</script>

Задания для самостоятельной работы

Задачи взяты из задачника Г. Н. Бермана. Номера задач мы сохраняем для того, чтобы можно было проверить результаты.

2347. Вычислить число π используя интеграл:.
Ответ: 3,1415926535897932384626433832795.

2348. Вычислить число π используя интеграл:
Ответ: 3,1415926535897932384626433832795.

2349. Вычислить
Ответ: 2,31.

2350. Вычислить приближенно
Ответ: 0,837.

2351. Вычислить приближенно
Ответ: 1,09.

2352. Вычислить приближенно
Ответ: 2,59.

2355. Вычислить приближенно
Ответ: 0,985.