Оглавление
Приближенное вычисление определенного интеграла
Метод средних прямоугольников
Создаем подпрограмму для вычисления интеграла от произвольной функции, заданной пользователем
<script type="text/javascript">
var a, b, n, f;
a = 2;
b = 5;
n = 100;
f = "1/log(x)";
integral(a, b, n, f);
function integral(a, b, n, f) {
var s, d, xb, xe, x, t;
s = 0;
d = (b - a)/n;
xb = a;
t = f;
f= "with (Math) {" + f + "}";
for(i = 0; i < n; i++){
xe = xb + d;
x = (xb + xe)/2;
s = s + d*eval(f);
xb = xe;
}
t = " Интеграл от " + t + " = " + s;
document.write(t);
}//function integral
</script>
Задание для самостоятельной работы
В качестве самостоятельной работы рекомендуется написать подпрограмму-функцию для вычисления определенного интеграла по методу Симпсона.
Окончательный вариант программы
Незначительная доработка позволяет получить симпатичную программу для вычисления интеграла от произвольного подынтегрального выражения с простым и ясным интерфейсом, которая приводится ниже.
Задание для самостоятельной работы
Используя программу, вычислить интегралы из задачника Г. Н. Бермана
2231. Вычислить приближенно 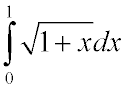
Ответ: 1,2189514164974600650689182989463.
2232. Вычислить приближенно 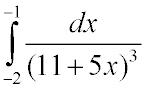
Ответ: 7/72.
2234. Вычислить приближенно 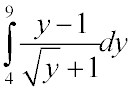
Ответ: 23/3.
2236. Вычислить приближенно 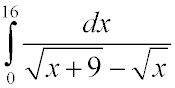
Ответ: 12.
2239. Вычислить приближенно 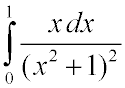
Ответ: 0,25.
2242. Вычислить приближенно 
Ответ: 1,069560557758917088511636683538.
2245. Вычислить приближенно 
Ответ: 4/3.
2251. Вычислить приближенно 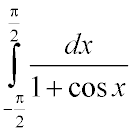
Ответ: 2.
2252. Вычислить приближенно 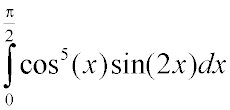
Ответ: 2/7.
2253. Вычислить приближенно 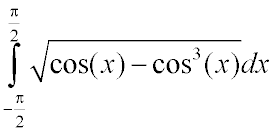
Ответ: 4/3.
2282. Вычислить приближенно 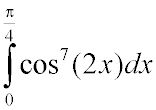
Ответ: 8/35.
2302. Вычислить приближенно 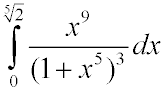
Ответ: 2/45.